Fourier-Reihen

Reele Darstellung

Mit Periode 2 Pi

Wir wollen eine periodische Funktion $f(x)$ mit der Periode $T=2\pi$ mit einer Überlagerung von trigonometrischen Funktionen annähern. Mit einer sog. Fourier-Reihe der folgenden Form

$\hat{f}(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}{a_n \cdot cos(nx)+b_n\cdot sin(nx)}$

Dafür müssen die sog. Fourierkoeffizienten so gewählt werden, dass es die Funktion am besten annähert. Diese kann man auch berechnen

$$\begin{align*} a_0&=\frac{1}{\pi}\cdot \int_0^{2\pi}{f(x)\,dx} \\ a_n&=\frac{1}{\pi}\cdot \int_0^{2\pi}{f(x)\cdot cos(nx)\,dx} \\ b_n&=\frac{1}{\pi}\cdot \int_0^{2\pi}{f(x)\cdot sin(nx)\,dx} \\ n&=1,2,3,... \end{align*}$$

Gerade Funktion

Wenn die Funktion $f(x)$ die wird approximieren gerade ist, also $f(-x)=f(x)$ so können wir die Berechnung von den Sinusglieder sparen. Die Fourier-Reihe hat dann nurnoch die folgende Form

$\hat{f}(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}{a_n \cdot cos(nx)}$

Ungerade Funktion

Bei ungeraden Funktion, also wenn $f(-x)=-f(x)$ können wir ähnlich die Kosinusglieder weglassen.

$\hat{f}(x)=\sum_{n=1}^{\infty}{b_n\cdot sin(nx)}$

Rechteckkurve

Wir wollen eine Fourier-Reihe der Rechteckskurve mit der Periode $T=2\pi$ bilden.

$$f(x)=\begin{cases} 1 &0\leq x \leq \pi\\ -1 &\pi < x < 2\pi \end{cases}$$

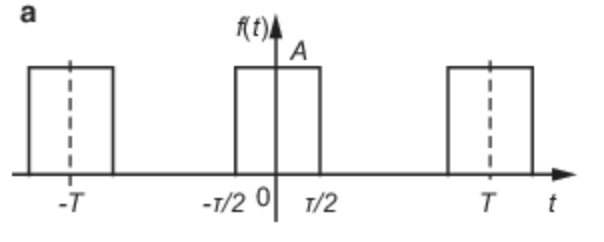
Die Funktion ist ungerade also können wir uns das Leben einfacher machen. das interessante ist bei der Berechnung das wir das Integral aufspalten können

$$\begin{align*} b_n &=\frac{1}{\pi}\cdot \int_0^{2\pi}{f(x)\cdot sin(nx)\,dx} \\ &=\frac{1}{\pi}\left[\int_0^\pi{1\cdot sin(nx)\,dx}+\int_\pi^{2\pi}{(-1)\cdot sin(nx)\,dx}\right] \end{align*}$$

Mit Periode T

Nicht immer ist unsere Periode $2\pi$ deshalb wollen wir eine allgemeine Formulierung für eine Periode mit dem Wert T. Wichtig ist hier das $T=\frac{2\pi}{\omega_0}$ und \omega_0 die sog. Kreisfrequenz der Schwingung ist.

$\hat{f}(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}{a_n \cdot cos(n\omega_0x)+b_n\cdot sin(n\omega_0x)}$

Daraus folgt dann

$$\begin{align*} a_0&=\frac{2}{T}\cdot \int_{(T)}{f(x)\,dx} \\ a_n&=\frac{2}{T}\cdot \int_{(T)}{f(x)\cdot cos(n\omega_0x)\,dx} \\ b_n&=\frac{2}{T}\cdot \int_{(T)}{f(x)\cdot sin(n\omega_0x)\,dx} \\ n&=1,2,3,... \end{align*}$$

Wichtig dabei ist zu beachten, dass das Integrationsinterval die Länge der Periode hat.

Komplexe Darstellung

Mit Periode 2 Pi

Dank der Euler-Formel können wir die Fourier-Reihe auch in komplexer Form darstellen dafür müssen wir folgendes beachten

$cos(nx)=\frac{1}{2}(e^{inx}+e^{-inx})$

$sin(nx)=\frac{1}{2}i(e^{inx}+e^{-inx})$

Wir können so dann die Fourier-Reihe und die Koeffizienten Berechnung viel kürzer schreiben.

$$\begin{align*} \hat{f}&=\sum_{n=-\infty}^{\infty}{c_n\cdot e^{inx}} \\ c_n&=\frac{1}{2\pi}\cdot \int_0^{2\pi}{f(x)\cdot e^{-inx}\,dx} \\ n&=0,\pm 1,\pm 2,\pm 3,... \end{align*}$$

Mit Periode T

Auch hier können wir die Formel umschreiben damit wir eine beliebige Periode $T$ verwenden können.

$$\begin{align*} \hat{f}&=\sum_{n=-\infty}^{\infty}{c_n\cdot e^{in\omega_0x}} \\ c_n&=\frac{1}{T}\cdot \int_0^T{f(x)\cdot e^{-in\omega_0x}\,dx} \\ n&=0,\pm 1,\pm 2,\pm 3,... \end{align*}$$

Zusammenhang reele und komplexe Darstellung

Wir können die Koeffizienten von der einen Darstellung in die andere Darstellung umrechnen mit den folgenden Formeln

Reele zu komplexe

$c_0=\frac{1}{2}a_0, \quad c_n=\frac{1}{2}(a_n-ib_n), \quad c_{-n}=\frac{1}{2}=(a_n+ib_n)$

Komplexe zu reele

$a_0=2c_0, \quad a_n=c_n+c_{-n}, \quad b_n=i(c_n-c_{-n})$