Kovarianz

Die Kovarianz ist wie die Varianz und die Kovarianz eine Kennzahl. Die Kovarianz kann genutzt werden für die Überprüfung ob es zwischen zwei Zufallsvariablen lineare Zusammenhänge gibt oder nicht. In anderen worte ob die eine Zufallsvariable mit der anderen zu tun hat. Die Kovarianz kann jedoch keine genaue Aussage zur Abhängigkeit machen!

$Cov(X,Y) = E((X - E(X))*(Y-E(Y)))$

Oder mehr mathematisch ausgedruckt aber nur für diskrete Zufallsvariablen mit $N$ werte:

$Cov(X,Y) = \frac{1}{N} \sum_{i=1}{n}{(x_i - E(X))\cdot(y_i - E(Y))}$

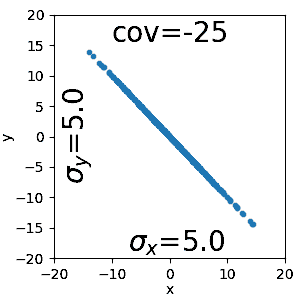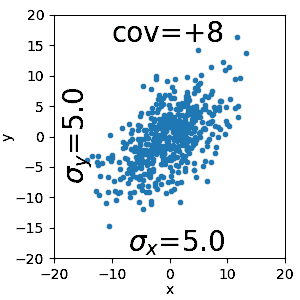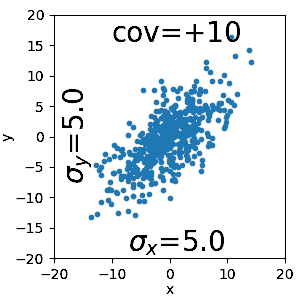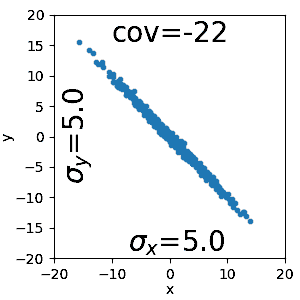
Multivariate Normalverteilung

Die multivariate Normalverteilung ist sehr ähnlich wie die eindimensionale Normalverteilung. Sie verallgemeinert die eindimensionalen Normalverteilung auf mehrere Dimensionen. Anstatt Erwartungswert und Standardabweichung hat die multivariate Normalverteilung folgende Parameter:

• Der Erwartungswertvektor $\mu$
• Die Kovarianzmatrize $\Sigma$
• Wir schreiben dann für eine $p$-dimensionale Zufallsvariable $X \sim N_p[\mu,\Sigma]$
• Die Dichte von $X$ ist $f_{\mu,\Sigma}(x)= \frac{1}{\sqrt{(2\pi)^p \mathbb{det}(\sigma)}} e^{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)}$

Genau wie bei der eindimensionale Normalverteilung haben die Parameter einen Einfluss auf die Form der Verteilung, vorallem die Kovarianzmatrize.

Mit einer zweidimensionalen Matrize $\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}$ sieht die Verteilung so aus: